Piyush Theorem #3 – ρiγush's mατhεmatιζs

सुई से लिखी मधुशाला ( मधुशाला )

सुई से लिखी मधुशाला ( Madhushala ) पीयूष ने एक ऐसा कारनामा कर दिखाया है कि देखने वालों आँखें खुली रह जाएगी और न देखने वालों के लिए एक स्पर्श मात्र ही बहुत है। पीयूष ने पूछने पर बताया कि सुई से पुस्तक लिखने का विचार क्यों आया ? अक्सर मुझ से ये पूछा जाता था कि आपकी पुस्तक

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी स

दुनिया का पहली हस्त लिखित चाणक्य नीति दर्पण छवि

६०० कैरीकैचर्स इन नए फ्रेम

६०० कैरीकैचर्स इन नए फ्रेमपीयूष गोयल अपनी धुन के पक्के हमेशा कुछ ना कुछ नया करते रहना उनकी फ़ितरत हैं. इसी के चलते पीयूष गोयल ने दुनिया की पहली मिरर इमेज किताब”श्री मदभगवदगीता” के सभी 18 अध्याय 700 श्लोक हिन्दी व अंग्रेजी दोनो भाषाओ में लिख चुके हैं कुछ समय पहले पीयूष ने

कील से लिखी 'पीयूष वाणी'

कील से लिखी 'पीयूष वाणी' पीयूष ने अपनी ही लिखी पुस्तक 'पीयूष वाणी' को कील से ए-फोर साइज की एल्युमिनियम शीट पर लिखा है। पीयूष ने पूछने पर बताया कि कील से क्यों लिखा है ? तो उन्होंने बताया कि वे इससे पहले दुनिया की पहली सुई से स्वर्गीय श्री हरिवंशराय बच्चन जी की विश्व प्रसिद्ध पुस्तक 'मधुशाला' को

मेंहदी कोन से लिखी गई गीतांजलि ( गीतांजलि )

मेंहदी कोन से लिखी गई गीतांजलि ( गीतांजलि )पीयूष ने एक और नया कारनामा कर दिखाया है उन्होंने 1913 के साहित्य के नोबेल पुरस्कार विजेता रविन्द्रनाथ टैगोर की विश्व प्रसिद्ध कृति 'गीतांजलि' को 'मेंहदी के कोन' से लिखा है। उन्होंने 8 जुलाई 2012 को मेंहदी से गीतांजलि लिखनी शुरू क

थॉट्स ऑफ़ पियूष गोयल

1. भगवान श्री कृष्ण अर्जुन के ही सारथि नही थे वे तो पूरे विश्व के सारथि हैं ,फिर डर किसका 2. वर्तमान की आवश्यकता भविष्य की निधि हैं. 3. किसी भी कार्य के पर्याय बन जाओ प्रसिद्धि अवश्य मिल जाएगी. 4. अपने सुखो को दूसरो के दूखो में बाँट दो. 5. जीवन में लक्ष्य ज़रूर निर्धारित करो लक्ष्य मिलने पर आकर

ऑटोग्राफ ऑफ़ ऐ॰ पी॰ जे॰ अब्दुल कलाम जी

ऑटोग्राफ़ ऑफ़ अमिताभ बच्चन

​

दर्पण छवि के लेखक पीयूष गोयल

 1.पीयूष जी अपने बारे में बताए. जी मेरा नाम पीयूष कुमार गोयल है में पिता डाक्टर देवेंद्रा कुमार गोयल व माता रवि कांता गोयल का बड़ा बेटा हूँ मे डिप्लोमा यांत्रिक इंजिनियर हूँ और एक कंपनी में कार्यरत हूँ. 2.पीयूष जी आपने इतना सुंदर काम किया हैं इस की प्रेरणा कहा से मिली ? जी सच तो ये हैं मुझे ईश्वर

ऑटोग्राफ ऑफ़ हेमा मालनी

​

ऑटोग्राफ ऑफ़ विश्व नाथ प्रताप सिंह

ऑटोग्राफ ऑफ़ सचिन तेंदुलकर

ऑटोग्राफ ऑफ़ जावेद अख्तर

माउस द्वारा बनाया गया

दिल से लिखे ई लव माय इंडिया

पियूष थियोरम

Write down 0,1,2,3,4,5 and put parallel square of each number like 0,1,4,9,16,25, then start to subtract the bigger one to the lower one (1–0),(4–1),(9–4),(16–9) and (25–16) to get 1,3,5,7,9 and again subtract the bigger one to the lower one (3–1),(5–3),(7–5) and (9–7) to get (2,2,2,2). Again we sq

A New Theorem introduced by Piyush Goel with Four Proofs – ρiγush's mατhεmatιζs

Mathematics for Piyush is a Passion from his childhood he was so passionate about Mathematics used to play with Numbers draw figures and try to get sides distance one day I draw a AP SERIES Right Angle Triangle( thinking that the distance between the point of intersection

A new method of squaring and cubing – ρiγush's mατhεmatιζs

Below we demonstrate a simple method to find nth power of a number. Here we’ll take examples to find Square & Cube of a number through Points marked on 2 faces & 3 faces of a Triangular Pyramid respectively.Firstly, we are finding cube of a number.We take 3 Pyramid faces

A note on the Factorial Function – ρiγush's mατhεmatιζs

Write down 0,1,2,3,4,5 and put parallel square of each number like 0,1,4,9,16,25, then start to subtract the bigger one to the lower one (1–0),(4–1),(9–4),(16–9) and (25–16) to get 1,3,5,7,9 and again subtract the bigger one to the lower one (3–1),(5–3),(7–5) and (9–7) t

Amazing Number Nine – ρiγush's mατhεmatιζs

IT IS VERY INTERESTING TAKE ANY NUMBER OF DIGITS. HERE I AM TAKING 25 AND 32YOU CAN WRITE THEM IN FOUR WAYS LIKE THAT(25*32/25*23/52*23/52*32)25*32=80025*23=57552*23=119652*32=1664SUBTRACT BIGGER ONE TO ANY LOWER, ONE BY ONE1664-1196=468=4+6+8=­18=1+8=91664-575=1089=1+0+8

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

पीयूष गोयल ने बनाये 600 केरिकेचर्स

पीयूष गोयल अपनी धुन के पक्के हमेशा कुछ ना कुछ नया करते रहना उनकी फ़ितरत हैं. इसी के चलते पीयूष गोयल ने दुनिया की पहली मिरर इमेज किताब"श्री मदभगवदगीता" के सभी 18 अध्याय 700 श्लोक हिन्दी व अंग्रेजी दोनो भाषाओ में लिख चुके हैं कुछ समय पहले पीयूष ने सुईं से भी किताब लिखी हैं

New Squaring Method – ρiγush's mατhεmatιζs

New Squaring Method – ρiγush's mατhεmatιζs

Square through Squares – ρiγush's mατhεmatιζs

Square through Squares – ρiγush's mατhεmatιζs

Piyush Goel

Piyush Goel

मधुशाला दर्पण छवि में लिखने के लिए सम्मान

इंटरव्यू लोकसभा पर

If God Is..........

If God Is.......... Author: पियूष गोयल If God is Parents. I Adore. If God is Brother & Sister. I Love & Share. If God is Children. I Kiss. If God is Wife. I Love & Have Faith. If God is Life. I Care. If God is Success. I Accept. If God is Night. I Sleep. If

Bio-Profile of Piyush Goel | World Hindu News

Piyush Goel, born on 10th February, 1967, Aquarian, belongs to a middle class family, elder son of Dr. Devender Kumar Goel and Ravikanta. He is Diploma Mechanical Engineering, Diploma in Material Management, Diploma in Vastu Shastra and Diploma in Business Management. Cre

Inspirational Story about Piyush Goel - Mirror Image Man

A dream doesn’t become reality through magic; it takes sweat, determination and hard work. एक सपना जादू से हकीकत नहीं बन सकता ; इसमें पसीना , दृढ संकल्प और कड़ी मेहनत लगती है .From his early childhood he was so creative, full of imagination and firm believ

Piyush Goel (writer)

Piyush Goel (writer)

Piyush Goel -Mirror Image Man | साहित्य संहिता

1.ShreeMadBhagvadGita in Hindi Language (Pen). 2.ShreeMadBhagvadGita in English Language (Pen). 3.Shree Durga Saptsatti in Sanskrit Language (Pen). 4.Shree Sai Satcharitra in Hindi Language (Pen). 5.Shree Sai Satcharitra in English Language (Pen). 6&7. Sunder Kand (2 tim

Squaring: A New Way - Gonit Sora

If we square 11, it is very simple put 1(2*1)(12)get 121 same as square 12 put 1(2*2)(22) get 144 again for 13 we get 169 and for 14 we get 1 8 16=196 and so on.When we go deep, we find that there is symmetry of two types(2,4,6,8,10,12 ,14,16,18,20 …. Diff is always 2) &(

lámparas : Piyush Goel Ordinary Indian Man With Extraordinary Achievement Foto

Piyush Goel Ordinary Indian Man with Extraordinary Achievement lámparas : Piyush Goel Ordinary Indian Man With Extraordinary Achievement Foto

भगवद गीता इन मिरर इमेज

Bhagwad Gita in Mirror ImagePiyush Goel has written Bhagwad Gita in mirror image.Who was he motivated to take upon such an unique way? He says that in the year 2000 an accident changed his life. In 2003 there was a Katha organized on Shreemad Bhagwad Gita , he used to go

Bhagwad Gita in mirror image – Piyush Goel | World Hindu News

Piyush GoelPiyush Goel has written Bhagwad Gita in mirror image. Who was he motivated to take upon such an unique way? He says that in the year 2000 an accident changed his life. In 2003 there was a Katha organized on Shreemad Bhagwad Gita , he used to go daily two times

unique art : piyush goel introduced mirror image writing style

unique art : piyush goel introduced mirror image writing styleलेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयूष वाणी लिख डाली। पीयूष की इन किताबों को देखकर हर कोई हतप्रभ है।कला और दक्षता की कोई स

Bhagwad Gita Written in Mirror Image by Piyush Goel | SpeakBindas

Piyush Goel a resident of Dadri has written Bhagwad Gita in mirror image. Ho was he motivated to take upon such an unique way? He says that in the year 2000 an accident changed his life. In 2003 there was a Katha organized on Shreemad Bhagwad Gita , he used to go daily tw

Piyush Goel – an ocean of talent | SpeakBindas

Piyush Goel has written Bhagwad Gita in mirror image. Who was he motivated to take upon such an unique way? He says that in the year 2000 an accident changed his life. In 2003 there was a Katha organized on Shreemad Bhagwad Gita, he used to go daily two times, on the las

Chankya Niti written with the help of Ink and Wooden Pen | SpeakBindas

1.ShreeMadBhagvadGita in Hindi Language (Pen). 2.ShreeMadBhagvadGita in English Language (Pen). 3.Shree Durga Saptsatti in Sanskrit Language (Pen). 4.Shree Sai Satcharitra in Hindi Language (Pen). 5.Shree Sai Satcharitra in English Language (Pen). 6&7. Sunder Kand (2 tim

My Mathematics Passion – Piyush Goel | SpeakBindas

3. Piyush Formula And Table For SquaringBelow we demonstrate a simple method to find nth power of a number. Here we’ll take examples to find Square & Cube of a number through Points marked on 2 faces & 3 faces of a Triangular Pyramid respectively.Firstly, we are finding c

Four Proof of Theorem By PIYUSH GOEL | SpeakBindas

Four Proof of Theorem (By PIYUSH GOEL)Piyush Theorem: In a Right-Angled Triangle with sides in A.PTheorem: In a Right-Angled Triangle with sides in A.P. Series, the distance between the point of intersection of median & altitude at the base is 1/10 Th the sum of other two

पीयूष गोयल ने बनाये 600 केरिकेचर्स - KhabarTak

पीयूष गोयल अपनी धुन के पक्के हमेशा कुछ ना कुछ नया करते रहना उनकी फ़ितरत हैं. इसी के चलते पीयूष गोयल ने दुनिया की पहली मिरर इमेज किताब”श्री मदभगवदगीता” के सभी 18 अध्याय 700 श्लोक हिन्दी व अंग्रेजी दोनो भाषाओ में लिख चुके हैं कुछ समय पहले पीयूष ने सुईं से भी किताब लिखी हैं

मिरर इमेज लिखने के शोक से रचा इतिहास |

लखनऊ। सेल्फी में आपके बायें गाल का तिल, आपकी दायीं गाल पर दिखता है। आईने में भी ऐसा ही होता है। इसे मिरर इमेज कहते हैं। दादरी के पीयूष गोयल लिखते मिरर इमेज में हैं। यानी इनकी किताबें पढऩे के लिए दर्पण की जरूरत होगी। पीयूष ने प्रसिद्ध ग्रंथों को मिरर इमेज में लिखा है। उल्ट

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

क्रिकेट के भगवान केसे कहलाये सचिन तेंदुलकर -कमलेश कुशवाह दोस्तों आज में आपको जिस शख्स की biography in hindi बताने वाला हु,वोह किसी परिचय के मोहताज नहीं है,इन्होने कई records बनाए है,एक ऐसे शख्स जिसने शावित कर दिया है की अगर हममे किसी भी काम के प्रति सच्ची लगन हो तोह कुछ भ

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसिद्ध पुस्तकें

दुनिया में एक से एक कलाकार मौजूद हैं जिनकी प्रतिभा देखकर लोग इसे चमत्कार समझने लगते हैं। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौंका दिया है। लेख क पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्

पियूष गोयल के विचार

Mirror Image Writer- Piyush Goel

Piyush Goel Mirror Image WriterPiyush Goel, born on 10th February, 1967, Aquarian, belongs to a middle class family, elder son of Dr. Devender Kumar Goel and Ravikanta. He is Diploma Mechanical Engineering, Diploma in Mate

Piyush Theroem | Mathematics Theorems Wiki | Fandom powered by Wikia

Piyush Theorem: In a Right-Angled Triangle with sides in A.PTheorem: In a Right-Angled Triangle with sides in A.P. Series, the distance between the point of intersection of median & altitude at the base is 1/10 Th the sum of other two sides.This Theorem applies in Two Con

Piyush Theroem | Mathematics Theorems Wiki | Fandom powered by Wikia

Piyush Theorem: In a Right-Angled Triangle with sides in A.PTheorem: In a Right-Angled Triangle with sides in A.P. Series, the distance between the point of intersection of median & altitude at the base is 1/10 Th the sum of other two sides.This Theorem applies in Two Con

माय STAMPS

संग्रह प्रदर्शनी

साक्षात्कार लोकसभा पर

सम्मान समारोह

पंचतंत्र और मधुशाला को पियूष का नया कलेवर, हादसे के दौरान मिली प्रेरणा | ekhabar.in | ekhabar

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

Mirror Image लिखने के शौक ने लिखवाई विश्व प्रसिद्ध पुस्तकें – Lcn News

Mirror Image लिखने के शौक ने लिखवाई विश्व प्रसिद्ध पुस्तकेंMirror Image लिखने के शौक के कारण विश्व प्रसिद्ध पुस्तकें लिख डालीं। दुनिया में एक से एक कलाकार मौजूद हैं जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते हैं। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौंका दिय

भगवद् गीता पेन से, मधुशाला सुईं से, गीतांजलि मेहन्दी कोन से लिखी

जिंदगी एक हादसों भरा सफ़र है। कई बार ये हादसे एक इंसान की जिंदगी बदल देते हैं। बदलाव कैसा होता है ये उस इन्सान पर निर्भर करता है जिसके साथ ये हादसा हुआ है। ऐसा बहुत कम देखा जाता है कि किसी हादसे के बाद इन्सान आगे बढ़ने की हिम्मत करे। उसकी जिंदगी गुमनामियों में कहीं खो जाती

World Famous Books Written In Mirror Image - Blog Trumpet

World Famous Books Written In Mirror Image1.Mirror Imaged Shree Mad BhagvadGita (Pen)-Piyush Goel has a unique art, he can write words in mirror image.Piyush Goel can write words in mirror image in two languages Hindi and English.He has completed “World First Mirror Image

तू ही सच्चा उत्तराधिकारी हैं.................

तू ही सच्चा उत्तराधिकारी हैं................. घने जंगलों में एक ज्ञानी ऋषि अपने कुछ शिष्यों के साथ एक कुटियाँ में रहते थे,ऋषि पहुचे हुएँ थे,उन्हें अपने उत्तराधिकारी का चुनाव करना उन्होनें अपने शिष्यों को बुलाया एक-एक हीरा देकर कहा की इनमें एक हीरे का वजन कुछ हल्का हैं. हा

दुख में ही भगवान को.........

दुख में ही भगवान को.........बहुत पुरानी बात हैं,किशनगढ़ के राजा ने अपनी प्रजा की नियत के बारे में पता लगाने के लिए सेनापति को बुलाया और एक आदेश पारित किया की सुखो व दुखो की पोटलिया बनाकर गाँवो के एक-एक मंचो पर रख दी जायें और ढिढोरा पिट वा कर पोटलियों को उठाने के लिए कहा ज

मंज़िल

मंज़िल अ मेरी मंज़िल आ राहों मेंइक दिन चल पड़ूँगाउस तरफओर मंज़िल मुझे मिल जायेगीऔर अंत मेंअस्त हो जाउगा.

काश

काशकाश, मेरा ज्ञान सूरज बन जाता चारो ओर प्रकाश फेलाता /काश,मेरा अज्ञान धुआ बन जाता ओर आकाश में कही गुम हो जाता/काश,मेरा घमंड काँच बन जाता टकराते ही चूर-चूर हो जाता /काश,मेरा आलस्यापतंग बन जाता ओर डोर हाथ से टूट जाता/काश, मेरा विश्वासचट्टान बन जाता तोड़ने पर टूट न पता/काश,मेरी छाया परछाई बन जाती सुब

ρiγush's mατhεmatιζs – – Dr. Piyush Goel

Mathematics for Piyush is a Passion from his childhood he was so passionate about Mathematics used to play with Numbers draw figures and try to get sides distance one day I draw a AP SERIES Right Angle Triangle( thinking that the distance b

ρiγush's mατhεmatιζs – – Dr. Piyush Goel

Mathematics for Piyush is a Passion from his childhood he was so passionate about Mathematics used to play with Numbers draw figures and try to get sides distance one day I draw a AP SERIES Right Angle Triangle( thinking that the distance between the point of intersection

Piyush Theorem #3 – ρiγush's mατhεmatιζs

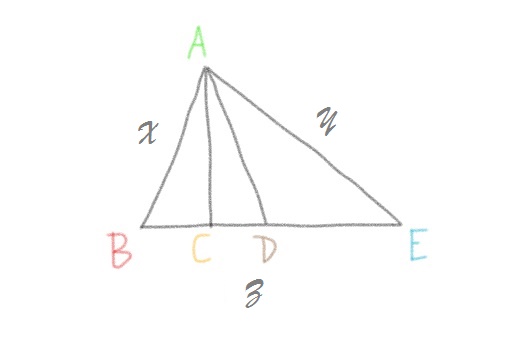
Statement: In a Right-angled ◺ Triangle, if distance between middle point and perpendicular point and sum of other two sides is divisible by 10, then sides will be in A.P. Series.As per FigureZ^2=X^2 +Y^2X^2 = AC^2 + BC^2 X^2 = AC^2 + (Z/2 – X+Y/10)Y^2 = AC^2 + CE^2

सबरंग,मेरठ से प्रकाशित

दिव्या मराठी में प्रकाशित

सिटी प्लस में प्रकाशित

पियूष गोयल के विचार

इ

पियूष गोयल थॉट्स

पीयूष गोयल जिन्होंने पाँच अदभुत तरीकों से लिखी है पुस्तकें - YouTube

पीयूष गोयल- जिन्होंने पाँच अदभुत तरीकों से लिखी है पुस्तकेंउल्‍टे अक्षरों से लिख गई भागवत गीता (Bhagwat Gita)आप इस भाषा को देखेंगे तो एकबारगी भौचक्के रह जायेंगे। आपको समझ में नहीं आयेगा कि यह किताब किस भाषा शैली में लिखी हुई है। पर आप जैसे ही दर्पण ( शीशे‌ ) के सामने पहुं

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें...  | YUGVARTA NEWS

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

unique art : piyush goel introduced mirror image writing style

unique art : piyush goel introduced mirror image writing styleलेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयूष वाणी लिख डाली। पीयूष की इन किताबों को देखकर हर कोई हतप्रभ है।कला और दक्षता की कोई स

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

मिरर इमेज के शौक ने दिलाई पहचान, लिखी विश्व प्रसिद्ध पुस्तकें - Virat Post

पीयूष गोयल, जिन्होंने उल्टे अक्षरों में गीता, सूई से मधुशाला, मेहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र और कील से लिखी पीयूष वाणीनई दिल्ली। दुनिया में एक से एक कलाकार मौजूद हैं जिनकी प्रतिभा देखकर लोग इसे चमत्कार समझने लगते हैं। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों

पीयूष गोयल की पाँच तरीके से लिखी गई पाँच पुस्तकें : - रचनाकार

आइए, आज आपको एक ऐसी शख्सियत से मिलवाते हैं जिन्होंने विविध व आश्चर्यजनक तरीके से लेखन किया है.उल्‍टे अक्षरों से लिख गईभागवत गीता ( Bhagwat Gita )आप इस भाषा को देखेंगे तो एकबारगी भौचक्के रह जायेंगे। आपको समझ में नहीं आयेगा कि यह किताब किस भाषा शैली में लिखी हुई है। पर आप ज

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसिद्ध पुस्तकें ! – Samachar Today

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

पीयूष गोयल (कलाकार) - भारतकोश, ज्ञान का हिन्दी महासागर

पीयूष गोयल (अंग्रेज़ी:Piyush Goel) का जन्म 10 फ़रवरी1967 को माता रविकांता एवं डॉ. दवेंद्र कुमार गोयल के घर हुआ। पीयूष 2000 से कुछ न कुछ लिखते आ रहे हैं श्रीमदभगवदगीता (हिन्दी व अंग्रेज़ी), श्री दुर्गा सप्त सत्ती (संस्कृत), श्रीसांई सतचरित्र (हिन्दी व अंग्रेज़ी), श्री सुंद

उल्‍टे अक्षरों से लिखने में माहिर हैं पीयूष गोयल | Report4India

कई महत्वपूर्ण किताबें उल्टे अक्षर (मिरर इमेज शैली) में लिखींपीयूष गोयलपेन की जगह कील, सुई, कार्बन पेपर, मेहंदी कोन से आसानी से उल्टे अक्षर से लिख देतें हैं महत्वपूर्ण किताबेंनई दिल्ली। ‘करत-करत अभ्यास के जड़मति होत सुजान, रसरी आवत-जात ते सिल पर पड़त निशान’ का संदेश कर्म

एक हादसे से 'पीयूष गोयल' को मिला कुछ अलग करने का जज्बा - iBlogger.in : सर्वश्रेष्ठ हिंदी ब्लॉग और भारतीय ब्लॉगर

हमारे देश में एक से बढ़कर एक प्रतिभाएं मौजूद है जिनकी प्रतिभा लोगो को दॉतों तले उंगली दबाने को मजबूर कर देती है। ऐसी ही एक प्रतिभा है दादरी के पीयूष गोयल, जिन्होने ऐसा कारनामा कर दिखाया है कि देखने वालों आँखें खुली रह जाए। पियूष ने पांच तरह की पुस्तकों को उल्टे अक्षरों में

Thoughts of Piyush Goel - Nayi Kranti

पीयूष गोयल पेशे से डिप्लोमा यांत्रिक इंजिनियर है और एक बहुराष्ट्रीय कम्पनी में कार्यरत हैं। इन सबके अलावा पीयूष गोयल दुनिया की पहली मिरर इमेज पुस्तक श्रीमदभागवत गीता के रचनाकार हैं। पीयूष गोयल ने सभी 18 अध्याय 700 श्लोक अनुवाद सहित हिंदी व अंग्रेज़ी दोनों भाषाओं में लिखा

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

पीयूष गोयल ने बनाये 600 केरिकेचर्स

पीयूष गोयल अपनी धुन के पक्के हमेशा कुछ ना कुछ नया करते रहना उनकी फ़ितरत हैं. इसी के चलते पीयूष गोयल ने दुनिया की पहली मिरर इमेज किताब"श्री मदभगवदगीता" के सभी 18 अध्याय 700 श्लोक हिन्दी व अंग्रेजी दोनो भाषाओ में लिख चुके हैं कुछ समय पहले पीयूष ने सुईं से भी किताब लिखी हैं

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

Pythagorean Theorem from “a new angle”

Pythagorean Theorem from “a new angle”

Dr. Piyush Goel at India Book of Records

Dr. Piyush Goel at India Book of Records

Inspirational Quotes by Piyush Goel | Motivational Messages

1.The way you think the road you get.2.Love makes the way to God.3.Present is Past in Future.4.Pain is sure in Gain.5.In this world there are lot of Yesterdays, not many Tomorrows.6.Luck is a duck can Swim,Walk and Fly.7.Luck is as Lock you have its Key. Click left it,s c

Inspirational Story about Piyush Goel - Mirror Image Man

A dream doesn’t become reality through magic; it takes sweat, determination and hard work. एक सपना जादू से हकीकत नहीं बन सकता ; इसमें पसीना , दृढ संकल्प और कड़ी मेहनत लगती है .From his early childhood he was so creative, full of imagination and firm believ

Dont Give Up Member Piyush Kumar Goel The "Mirror Image Man" | | Dont Give Up World

Piyush Kumar Goel, an ordinary man from Greater Noida, India achieved some Extraordinary Achievement with his creativity andinnovative thinking. He is a mechanical engineer working in a private firm of Greater Noida, Dadri. Collecting unusual things is also hispassion. He

WORLD RECORD ASSOCIATION

The longest needle pricked book in the world Record properties: World Record Record source: World Record AssociationRecord Numbers: 50207-1301-01 The longest needle pricked book in the world——《Needle Book with 2 Lakhs Holes》From November 2010 to January 20

Bhagwad Gita Written in Mirror Image by Piyush Goel | SpeakBindas

Piyush Goel a resident of Dadri has written Bhagwad Gita in mirror image. Ho was he motivated to take upon such an unique way? He says that in the year 2000 an accident changed his life. In 2003 there was a Katha organized on Shreemad Bhagwad Gita , he used to go daily tw

पीयूष गोयल (कलाकार) - भारतकोश, ज्ञान का हिन्दी महासागर

पीयूष गोयल (अंग्रेज़ी:Piyush Goel) का जन्म 10 फ़रवरी1967 को माता रविकांता एवं डॉ. दवेंद्र कुमार गोयल के घर हुआ। पीयूष 2000 से कुछ न कुछ लिखते आ रहे हैं श्रीमदभगवदगीता (हिन्दी व अंग्रेज़ी), श्री दुर्गा सप्त सत्ती (संस्कृत), श्रीसांई सतचरित्र (हिन्दी व अंग्रेज़ी), श्री सुंद

Asian Records Academy

The Book Written with Henna Cone by an Individual (Male) was achieved by Piyush Goel Dadri Wala, Dadri, Uttar Pradesh, India on August 5, 2012. It counted to 68 pages of 103 different chapters. Asian Records Academy

कोरा कागज

कोरा कागज में एक कोरा कागज किसी के आँगन का यूँ ही फेक दिया जाता हूँ सड़क पर सड़ने के लिए उड़ने के लिए उठा ले जाएगा बेच देगा किसी कबाड़ीय को अपना पेट भरने के लिए जो यूँ की डाल देगा सड़े गले ढेरो में बेच देगा किसी और बड़े कबाड़ीय को अपना पेट भरने के लिए जाने कब तक यूँ ही

जिंदगी

 जिंदगीबचपन बड़ा होता हैं आँगन मेंऔर आँगन मेंतैरती हैं नावउड़ती हैं पतंगखेलते हैं खिलोनेआ जाते हैं राहों मेंऔर राहें मिलती हैंतिरहों परचोरहो परऔर एक दिन येंराहेंफँस जाती हैं जाम में(जिंदगी)पीयूष गोयल http://www.piyushgoel.in

भगवद् गीता पेन से, मधुशाला सुईं से, गीतांजलि मेहन्दी कोन से लिखी – Lokhit Khabar

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें - FreakyFuntoosh.com

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल (Piyush Goyal) ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ

सीरी फोर्ट स्टेडियम

दर्पण छवि में पुस्तके लिखने के लिए सम्मान

उल्टे अक्षरों में सुई, मेहंदी कोण और कील से लिख डाली, श्रीमद्भगवद्गीता सहित कई किताबें

नोएडा के पीयूष गोयल ने उल्टे अक्षरों में श्रीमद्भगवद्गीता, मधुशाला, गीतांजलि, लिखी है.लीक-लीक कायर चलें, लीकहिं चले कपूत लीक छोड़ तीनों चलें – शायर सिंह सपूत।लोकजीवन का यह प्रचलित दोहा नोएडा के 50 वर्षीय पीयूष गोयल की लाइफ पर फिट बैठता है. कहते हैं जिंदगी में जब कोई कुछ अ

A New way, The Area of Trapezium – ρiγush's mατhεmatιζs

Lot of mathematicians have proved Pythagoras theorem in their own ways. If you google it you will indeed found hundred of ways.Meanwhile I was also sure that maybe one day I could find something new out of this incredible Pythagoras theorem

Incredible Art - "Piyush Vani" with Glue and Gum

Incredible Art - "Piyush Vani" with Glue and Gum Incredible Art - "Piyush Vani" with Glue and Gum. Get to know all about Most Amazing Ideas, Quotes, Places, Funny Photos of Funny Animals, Int

PK - WikiOmni

12 नवेंबर 2017 को दिल्ली के सिरी फ़ोर्ट अडिटोरियम में करीब हजरू रेकॉर्ड्स होल्डर्स को अपने अपने रेकॉर्ड्स के लिए सम्मानित किया गया इसमे पीयूष गोयल को भी उनके रेकॉर्ड भगवद् गीता को दर्पण छवि में व सुई से लिखी दुनिया के पहली पुस्तक मधुशाला को भी वर्ल्ड रेकॉर्ड के लिए पदक दे

World First Hand Write Mirror Image Books Bhagwad Gita,Madhushala,Gitanjali,Panchtantra and Piyush Vani By Piyush Goel - WikiOmni

Piyush Goel, born on 10th February, 1967, Aquarian, belongs to a middle class family, elder son of Dr. Devender Kumar Goel and Ravikanta. He is Diploma Mechanical Engineering, Diploma in Vastu Shastr,. Creative, believe in God, believe in love & friendship.Piyush Goel ha

Piyush Goel | torial

उल्‍टे अक्षरों से लिख गई भागवत गीता ( Bhagwat Gita )आप इस भाषा को देखेंगे तो...via piyushgoel.in Piyush Goel | torial

PiyushGoel on Flipboard

पीयूष गोयल अपनी धुन के पक्के हमेशा कुछ ना कुछ नया करते रहना उनकी फ़ितरत हैं. इसी के चलते पीयूष गोयल ने दुनिया की पहली मिरर इमेज किताब"श्री मदभगवदगीता" …12 नवेंबर 2017 को दिल्ली के सिरी फ़ोर्ट अडिटोरियम में करीब हजरू रेकॉर्ड्स होल्डर्स को अप

मिताली गोयल

मिताली गोयल

A New Theorem Introduced by Piyush Goel With Four Proof - Documents

A New Theorem introduced by Piyush Goel with Four Proof Mathematics for Piyush is a Passion from his childhood he was so passionate about Mathematics used to play with Numbers draw figures and try to get sides distance one day I draw a AP SERIES Right Angle Triangle( t

इंडिया बुक ऑफ रेकॉर्ड्स ने रेकॉर्ड्स होल्डर्स को किया सम्मानित

12 नवेंबर 2017 को दिल्ली के सिरी फ़ोर्ट अडिटोरियम में करीब हजरू रेकॉर्ड्स होल्डर्स को अपने अपने रेकॉर्ड्स के लिए सम्मानित किया गया इसमे पीयूष गोयल को भी उनके रेकॉर्ड भगवद् गीता को दर्पण छवि में व सुई से लिखी दुनिया के पहली पुस्तक मधुशाला को भी वर्ल्ड रेकॉर्ड के लिए पदक दे

22 स्क्वेरफीट(5.5फीट*4फीट) की लुडो

कुछ ना कुछ करने वाले पीयूष गोयल ने अपने बेटे हीमेश गोयल के साथ मिलकर 22 स्क्वेरफीट(5.5फीट*4फीट) की एक लुडो बोर्ड बनाया हैं. पीयूष गोयल कुछ ना कुछ करते रहते हैं पीयूष गोयल अब तक 16 विश्वा प्रसिद्ध पुस्तके दर्पण छवि में लिख चुके हैं,अलग अलग तरीके से1.श्रीमदभगवद् गीता (हि

Lines which always motivate Dr. Piyush Goel – ρiγush's mατhεmatιζs

Piyush Goel, born on 10th February, 1967, Aquarian, belongs to a middle class family, elder son of Dr. Devender Kumar Goel and Ravikanta. He is Diploma Mechanical Engineering, Diploma in Vastu Shastr,. Creative, believe in God, believe in love & friendship.Piyush Goel ha

PiyushGoel

PiyushGoel

Dr. Piyush Goel receiving Honorary Doctorate Degree by the University of World Records, London – ρiγush's mατhεmatιζs

Dr. Piyush Goel receiving Honorary Doctorate Degree by the University of World Records, London – ρiγush's mατhεmatιζs

ρiγush's mατhεmatιζs – – Dr. Piyush Goel

Mathematics for Piyush is a Passion from his childhood he was so passionate about Mathematics used to play with Numbers draw figures and try to get sides distance one day I draw a AP SERIES Right Angle Triangle( thinking that the distance between the point of intersection

मिरर इमेज लिखने के शोक ने लिखवाई विश्व प्रसीद पुस्तकें

दुनिया में एक से एक कलाकार मौजूद है जिनकी प्रतिभा देखकर लोग चमत्कार समझने लगते है। ऐसे ही एक कलाकार ने पांच तरह की पुस्तकों को लिखकर चौका दिया है। लेखक पीयूष गोयल ने उल्टे अक्षरों में गीता, सुई से मधुशाला, मेंहंदी से गीतांजलि, कार्बन पेपर से पंचतंत्र के साथ ही कील से पीयू

ρiγush's mατhεmatιζs – – Dr. Piyush Goel

§ π = 360? How is it possible? – ρiγush's mατhεmatιζs

Playing with Numbers…. – ρiγush's mατhεmatιζs

Numbers are Amazing and have Own ValueWhenever I have free time used to play with numbers and sometime I got very wonderful results, here is one more article for the mathematics passionate and scholars and my main aim is whatever I have, firmly believe in Sharing (DO NOT

Somewhere Every Number goes through Digit “9” – ρiγush's mατhεmatιζs

Somewhere Every Number goes through Digit “9” – ρiγush's mατhεmatιζs

Repetition of Numbers while Summation of Sequences – ρiγush's mατhεmatιζs

Counting (2,3,4 ….9) Here is very amazing result you will see while we do counting of 2,3,4…. and we get digits(sum) repeat itself and sum of all digits always Nine,as shown below1. Counting of 22 4 6 8 10 12 14 16 18 20 22 242 4 6 8 1 3 5 7 9 2 4 62+4+6+8+1+3+5+7+9=45=4

Repetition of Numbers while Summation of Sequences

Repetition of Numbers while Summation of Sequences

Triangle of Nine – ρiγush's mατhεmatιζs

We all know how great this number “9” is. It is remarkably known for its cyclic properties which results in beautiful mathematical patterns.You might also know that,The difference between a base-10 positive integer and the sum of its digits

Can you solve this? - Dr Piyush Goel - YouTube

Can you solve this? - Dr Piyush Goel Can you solve this? - Dr Piyush Goel - YouTube

पियूष गोयल होनोरेड फॉर मिरर इमेज मधुशाला

Recently, In an event organised by World Records University in collab with Indo-Vietnam Medical Board, Piyush Goel was honoured for his very famous work "Madhushala in Mirror Image Writing" once again. Piyush Goel honoured for Mirror Image Madhushala - YouTube

Different Irregular Hexagons, Same Area \ (•◡•) / – ρiγush's mατhεmatιζs

Different Irregular Hexagons, Same Area \ (•◡•) / – ρiγush's mατhεmatιζs

Piyush Theorem - mycreationsandimaginations.over-blog.com

PiyushTheorem: In a Right-Angled Triangle with sides in A.P. Series, the distance between the point of intersection of median & altitude at the base is 1/10 Th the sum of other two sides. This Theorem applies in Two Conditions: The Triangle must be Right-Angled. Its Sides

Gr8 work - YouTube

Gr8 work - YouTube

How to Success by Piyush Goel Dadriwala. - YouTube

Published on Jul 25, 2018Work on Few Points like Change Your Bad Habits,Patience,Passion, Focus on Target Always,Respect Elders and Encourage Youngers,read Autobiographies.... www.piyushgoel.in piyushtheorem.wordpress.com How to Success by Piyush Goel Dadriwala.

मिरर इमेज वर्ड्स

At Gandhi Polytechnic, Alumini Function Signing Autographs. Check the Speed -Mirror Writing in English Language - YouTube